参考 OI-Wiki 上 c-forrest 分类的,大佬果然还是大佬啊。
转移优化
利用常见技巧优化
树状数组/线段树优化 DP
CF883B The Bakery
利用问题结构优化
斜率优化 DP
P2900 [USACO08MAR] Land Acquisition G
初学斜率规划时看到这么多题解有点云里雾里的,在这里再推一遍。
https://www.luogu.com.cn/article/z9eh1cp4
我们发现对于矩形 \(i,j\) 满足 \(h_i\leq h_j,w_i\leq w_j\),那么选 \(j\) 的时候一定可以并购 \(i\),因此将 \(i\) 删去。
将剩下的矩形按照 \(h\) 从大到小排序,此时 \(w\) 从小到大。
因为如果合并的不是一段连续区间,那么中间未被合并的部分一定可以合并。所以我们每次合并一段连续区间就好了。
设 \(f_i\) 为买下前 \(i\) 块土地的最小费用。
法一:函数图像
我们将 \(y_j=h_jw_i+f_{j-1}\) 视作一个 \(f_{j-1}\) 和 \(h_j\) 为常量,\(w_i\) 为变量 的一次函数。
事实上需要对每个 \(w_i\) 维护直线 \(y_{1\sim i}\) 上对应的值中最小的一个。
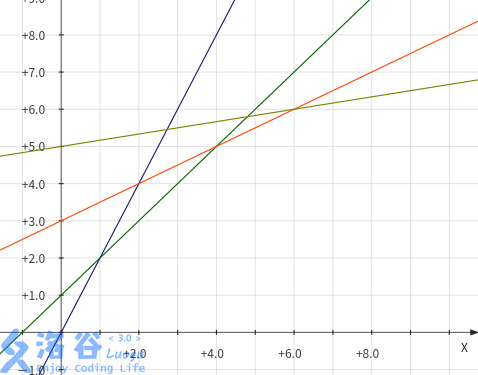
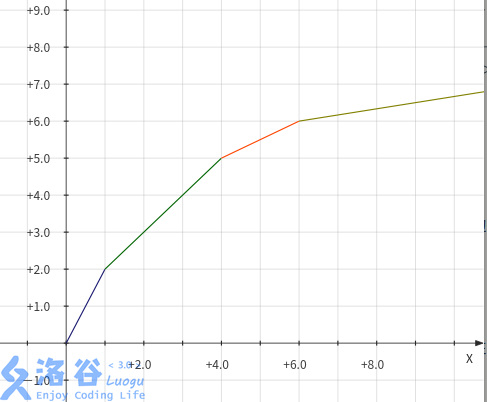
维护一个临界值 \(k\) 的单调队列。
每次加入一条直线时,斜率 \(h_j\) 递减,求得与队尾直线的临界点 \(k\)。
因为 \(w_i\) 递增,我们每次将队首临界值 \(k\leq w_i\) 的删除,队首即为最优决策。
法二:线性规划
\(f_i=\min\{h_jw_i+f_{j-1}\}\),相当于对于每个 \(j\) 有 \(f_{j-1}=-h_jw_i+t_j\),\(f_i=\min\{t_j\}\)。
我们把 \((-h_j,f_{j-1})\) 视作二维平面上一个点。
想象我们正拿着一个斜率为 \(w_i\) 的直线从下到上,遇到第一个时纵截距 \(f_i\) 取到最小值。
随便画一堆点就可以发现,无论直线以怎样的斜率向上靠,总有一些点永远都不会第一次与直线相交,也就是说这些决策是没用的。剩下的有用的决策点会构成一个凸包。
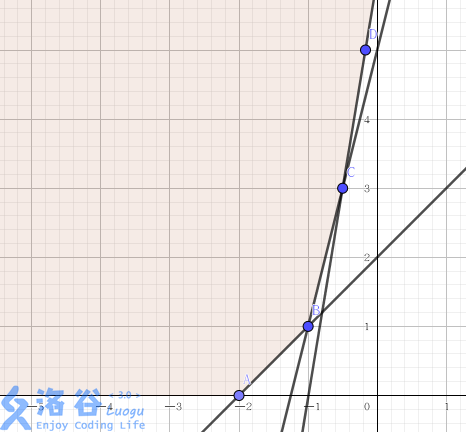
在此题中,因为 \(w\) 递增,所以我们的单调队列中存的是若干个点满足 \(-h_j\) 递增(即 \(h_j\) 递减),\(f_{j-1}\) 递增,而且相邻两个点的斜率也递增。
插入新决策点时可能会遇到下图情况:
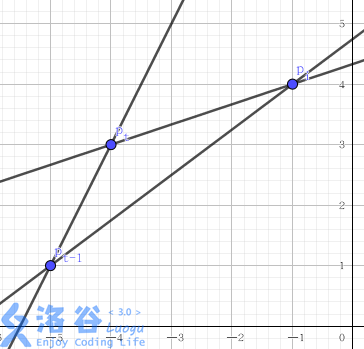
一直将队尾 \(t\) 出队,直到加入 \(i\) 后斜率仍递增。
我们再看回凸包那张图,手模一下,如果当前转移到 \(i\),一直将队首出队,直到队首和后一个的直线的斜率 \(>w_i\)。
此时队首即为能使 \(f_i\) 取得最小值的决策点。
法三:列出决策更优的条件
当前以 \(i\) 结尾,有任意决策点 \(j,k\) 满足 \(1 \leq j<k\leq i\),如果 \(i\) 比 \(j\) 更优,那么必定满足:
也即:
\(w\) 单调递增,我们维护一个斜率 \(\frac{f_{j+2}-f_{j+1}}{h_{j+1}-h_j}\) 单调递减(即为下凸)的队列。
易证不在队列中的一定不会成为最优决策点。
P3195 [HNOI2008] 玩具装箱
对于每个 j 的决策视为一条 \(y=(-2sum_j)x+(f_j+sum_j^2)\) 的直线。
\(k_p x + b_p \geq k_q x +b_q\)
\((k_p-k_q)x \geq b_q-b_p\)
\(x \geq -\frac{b_q-b_p}{k_q-k_p}\)